- PIs: Gambassi, Calabrese
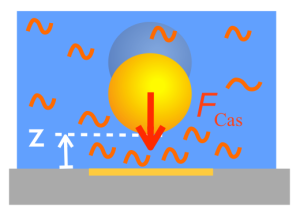
Fluctuations in classical statistical systems are typically negligible at the macroscopic scale. However, at shorter length scales or whenever collective behaviors emerge they may affect significantly the equilibrium and non-equilibrium behavior of these system, giving rise to novel phenomena such as fluctuation-induced forces (critical Casimir effect), aging, anomalous scaling and growth, etc. These phenomena play an important role and have relevant applications in a variety of interdisciplinary fields including soft matter, colloid and surface science, and population genetics.
Our research focuses on a number of aspects of these phenomena, which are largely unexplored, though being within experimental reach: non-equilibrium and many-body effects on the critical Casimir effect, interplay between critical and electrostatic fluctuations close to phase transitions, stochastic growth of interfaces and sufaces, aging phenomena after an abrupt temperature change in systems with physical boundaries, aging in the presence of colored noise, and effects of fluctuations on the dynamics of genes.
Advanced method of analysis include statistical field theory, boundary field theory, field-theoretical methods applied to stochastic processes, Monte Carlo and numerical simulations, statistical fluid dynamics, random matrix theory, replica Bethe ansatz, etc.

